This is a writeup of the problems my team solved in the Murcia contest, which we were participating in as preparation for SWERC. Those people are way better than us, but we will not give up!
The problems are given the UVa numbers that will soon appear.
12962 Average Reuse Distance
At first read this problem seems easier than it really is. But it’s not a hard problem, it’s actually a fairly straightforward simulation.
The Problem
Given a sequence of memory accesses to different addresses (represented by the
characters 'a' to 'z'), give its Average Reuse Distance. The Reuse Distance
of a memory access to address $x$ is the number of other addresses accessed
since the last access of $x$. First accesses to any given position do not count
towards the average.
The solution
The core of this problem was keeping track of the different memory accesses
since the last access of each address, and then counting them in an efficient
way. We solved this by storing which addresses had been accessed as a
bitmask. You can very easily reset the bitmask by setting it to 0, and count the
number of ones in the bitmask with GCC and Clang’s __builtin_popcount.
The algorithm is the following:
- Total sum = 0
- For each character $c$ of input read:
- If $c$ hasn’t been encountered before, mark it as encountered.
- Otherwise, add the number of ones in the bitmask to the total sum and add 1 to the number to divide the sum by.
- For all characters a-z, set their mask’s
th bit to 1. - Reset $c$’s bitmask to 0
In the end, you output the mean from the sum you gathered, or NaN if the divider is 0.
Here is the code.
12963 Astragalus Nitidiflorus
We technically did not solve this problem within the contest, but came very close. The night after the contest, when sitting down to look at the problems again, we found what was wrong in 5 minutes.
The problem
You are given a grid with characters on it. You have to find the horizontal instances of the word “GARBANCILLOS” and the vertical instances of the word “ASTRAGALUS”. Whenever they intersect is a possible location, but each word instance can only be used once. Determine the number of locations.
The grid is at most 150x150.
The solution
You need to do two things here. First, find the strings’ locations and where they intersect. Then, compute the maximum matching of vertical and horizontal strings.
To find the strings’ location in $\Theta(n^2)$, we used a rolling
hash. The longest of the strings is 12 characters, $12 \cdot 5 = 60 <
64$, so a hash with 5 bits per character can be used without
collisions. We discard all the characters outside of the range from
'A' to 'Z', and give them the mask 0x1f.
First we look at the character matrix horizontally, and store the
position of the found “GARBANCILLOS” in a sorted vector, one for each
row. We also store its future index in the graph of intersecting
strings in an std::map. Then we look at the character matrix vertically,
and when we find a match we binary search for the possible horizontal
matches in each row. If one is find, the edge is added to the
maximum-matching matrix.
Finally, we output the maximum matching of the matrix we built.
Here is the code.
12965 Angry Bids
Nice pun.
The problem
You have some product’s producers, and some consumers. Each of them has an ideal price. The consumers will get angry if the price is higher than their ideal price. The producers will get angry if the price is lower than their ideal price. Find the price such that the number of angry people is minimal, and how many angry people there are.
The prices range from $0$ to $10^9$. There are up to $10^4$ producers and $10^4$ consumers.
The solution
It’s amazing how many problems are solved this way. If we check every possible price in order (unfeasible), we will have more consumers progressively getting angry, and more producers progressively getting happy.
Thus, we assign producers the number 1, and consumers the number
-1. We create pairs of <price, assigned number> for each of them,
and sort those pairs. We increase the price of the consumers in the
pairs by 1 because that is when the consumer will start being
unhappy. We sort this sequence and then iterate over it, keeping a sum
of all the assigned numbers we have found. The point where this sum is
maximum is the optimal point.
Here is the code
12967 Spay Graphs
However, the name of the problem in the contest is “Spray Graphs”. And the page’s title is “Spary graphs”. Haha.
The problem
You are given the graph structure in the picture. In this picture, each “level” of the graph has an assigned letter. We can build more levels by branching every node in right angles as shown in the figure.
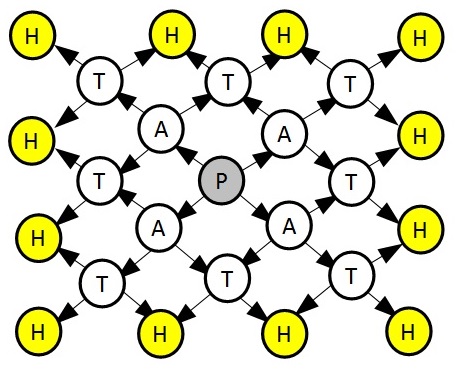
Spray graph of size 4 Problem by Facultad de Informática, Universidad de Murcia
Given a number of levels, compute how many paths there are to get to any of the leaves. The levels range from 1 to 30.
The solution
Notice two things about this graph. First, it has four-way symmetry around the central node, so we can just compute the paths of a quarter of the graph and then multiply by 4, we can get the answer.
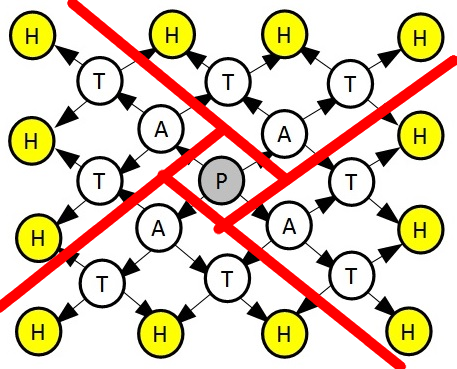
Radial symmetry in spray graphs
It is also very much like a grid, each node’s paths come only from the nodes to the left and up.
We can then build a grid with the number of paths for each node. The grid’s top row will be counting $1, 2, 3, …$ since the nodes in the top row of the separated portions in the previous picture have that number of paths. The first column will be all $1$s, since there is only one straight path down there. Then, we can compute each node’s number of paths as the paths coming from the left plus the paths coming from the top.
Here’s the grid for a size 5 graph:
| 1 | 2 | 3 | 4 |
|---|---|---|---|
| 1 | $2+1=3$ | $3+3=6$ | |
| 1 | $3+1=4$ | ||
| 1 |
Finally, just add up the leaves (the last diagonal), and multiply by 4. Bingo!
